Overview

SDDP.jl - Stochastic Dual Dynamic Programming in Julia.

SDDP.jl is a package for solving large multi-stage convex stocastic optimization problems. In this manual, we're going to assume a reasonable amount of background knowledge about stochastic optimization, the SDDP algorithm, Julia, and JuMP.

Types of problems SDDP.jl can solve

To start, lets discuss the types of problems SDDP.jl can solve, since it has a few features that are non-standard, and it is missing some features that are standard.

SDDP.jl can solve multi-stage convex stochastic optimizations problems with

• a finite discrete number of states;

• continuous state and control variables;

• Hazard-Decision (Wait-and-See) uncertainty realization;

• stagewise independent uncertainty in the RHS of the constraints that is drawn from a finite discrete distribution;

• stagewise independent uncertainty in the objective function that is drawn from a finite discrete distribution;

• a markov chain for temporal dependence. The markov chain forms a directed, acyclic, feed-forward graph with a finite (and at least one) number of markov states in each stage.

In this manual, we detail the many features of SDDP.jl through the classic example of balancing a portfolio of stocks and bonds over time.

Getting started

This package is unregistered so you will need to Pkg.clone it as follows:

Pkg.clone("https://github.com/odow/SDDP.jl.git")

If you want to use the parallel features of SDDP.jl, you should start Julia with some worker processes (julia -p N), or add by running julia> addprocs(N) in a running Julia session.

Formulating the problem

... still to do ...

For now, go look at the examples.

The Asset Management Problem

The goal of the asset management problem is to choose an investment portfolio that is composed of stocks and bonds in order to meet a target wealth goal at the end of the time horizon. After five, and ten years, the agent observes the portfolio and is able to re-balance their wealth between the two asset classes. As an extension to the original problem, we introduce two new random variables. The first that represents a source of additional wealth in years 5 and 10. The second is an immediate reward that the agent incurs for holding stocks at the end of years 5 and 10. This can be though of as a dividend that cannot be reinvested.

Communicating the problem to the solver

The second step in the optimization process is communicating the problem to the solver. To do this, we are going to build each subproblem as a JuMP model, and provide some metadata that describes how the JuMP subproblems inter-relate.

The Model Constructor

The core type of SDDP.jl is the SDDPModel object. It can be constructed with

m = SDDPModel( ... metadata as keyword arguments ... ) do sp, t, i
    ... JuMP subproblem definition ...
end

We draw the readers attention to three sections in the SDDPModel constructor.

Keyword Metadata

For a comprehensive list of options, checkout SDDPModel or type julia> ? SDDPModel into a Julia REPL. However, we'll briefly list the important ones here.

Required Keyword arguments

• stages::Int: the number of stages in the problem. A stage is defined as each step in time at which a decion can be made. Defaults to 1.

• objective_bound: a valid bound on the initial value/cost to go. i.e. for maximisation this may be some large positive number, for minimisation this may be some large negative number. You can ether pass a single value (used for all stages), a vector of values (one for each stage), or a vector of vectors of values (one vector for each stage, containing a vector with one element for each markov stage). Another option is to pass a function that takes two inputs so that f(t, i) returns the valid bound for stage t and markov state i.

• solver::MathProgBase.AbstractMathProgSolver: any MathProgBase compliant solver that returns duals from a linear program. If this isn't specified then you must use JuMP.setsolver(sp, solver) in the stage definition.

Optional Keyword arguments

• sense: must be either :Max or :Min. Defaults to :Min.

• cut_oracle: the cut oracle is responsible for collecting and storing the cuts that define a value function. The cut oracle may decide that only a subset of the total discovered cuts are relevant, which improves solution speed by reducing the size of the subproblems that need solving. Currently must be one of

  • DefaultCutOracle() (see DefaultCutOracle for explanation)

  • LevelOneCutOracle()(see LevelOneCutOracle for explanation)

• risk_measure: if a single risk measure is given (i.e. risk_measure = Expectation()), then this measure will be applied to every stage in the problem. Another option is to provide a vector of risk measures. There must be one element for every stage. For example:

risk_measure = [ EAVaR(lambda=0.5, beta=0.25), Expectation() ]

will apply the i'th element of risk_measure to every Markov state in the i'th stage. The last option is to provide a vector (one element for each stage) of vectors of risk measures (one for each Markov state in the stage). For example:

risk_measure = [
# Stage 1 Markov 1 # Stage 1 Markov 2 #
   [ Expectation(), Expectation() ],
   # ------- Stage 2 Markov 1 ------- ## ------- Stage 2 Markov 2 ------- #
   [ EAVaR(lambda=0.5, beta=0.25), EAVaR(lambda=0.25, beta=0.3) ]
   ]

Like the objective bound, another option is to pass a function that takes
as arguments the stage and markov state and returns a risk measure:

function stagedependentrisk(stage, markov_state)
    if state == 1
        return Expectation()
    else
        if markov_state == 1
            return EAVaR(lambda=0.5, beta=0.25)
        else
            return EAVaR(lambda=0.25, beta=0.3)
        end
    end
end

risk_measure = stagedependentrisk

Note that even though the last stage does not have a future cost function associated with it (as it has no children), we still have to specify a risk measure. This is necessary to simplify the implementation of the algorithm.

For more help see EAVaR or Expectation.

• markov_transition: define the transition probabilties of the stage graph. If a single array is given, it is assumed that there is an equal number of Markov states in each stage and the transition probabilities are stage invariant. Row indices represent the Markov state in the previous stage. Column indices represent the Markov state in the current stage. Therefore:

markov_transition = [0.1 0.9; 0.8 0.2]

is the transition matrix when there is 10% chance of transitioning from Markov state 1 to Markov state 1, a 90% chance of transitioning from Markov state 1 to Markov state 2, an 80% chance of transitioning from Markov state 2 to Markov state 1, and a 20% chance of transitioning from Markov state 2 to Markov state 2.

do sp, t, i ... end

This constructor is just syntactic sugar to make the process of defining a model a little tidier. It's nothing special to SDDP.jl and many users will be familiar with it (for example, the open(file, "w") do io ... end syntax for file IO).

An anonymous function with three arguments (sp, t and i, although these can be named arbitrarily) is constructed. The body of the function should build the subproblem as the JuMP model sp for stage t and markov state i. t is an integer that ranges from 1 to the number of stages. i is also an integer that ranges from 1 to the number of markov states in stage t.

Users are also free to explicitly construct a function that takes three arguments, and pass that as the first argument to SDDPModel, along with the keyword arguments. For example:

function buildsubproblem!(sp::JuMP.Model, t::Int, i::Int)
    ... define states etc. ...
end
m = SDDPModel(buildsubproblem!; ... metadata as keyword arguments ...)

JuMP Subproblem

In the next sections, we explain in detail how for model state variables, constraints, the stage objective, and any uncertainties in the model. However, you should keep a few things in mind:

1. the body of the do sp, t, i ... end block is just a normal Julia function body. As such, standard scoping rules apply.

2. you can use t and i whenever, and however, you like. For example:

m = SDDPModel() do sp, t, i
    if t == 1
        # do something in the first stage only
    else
        # do something in the other stages
    end
end

1. sp is just a normal JuMP model. You could (if so desired), set the solve hook, or add quadratic constraints (provided you have a quadratic solver).

State Variables

We can define a new state variable in the stage problem sp using the @state macro:

@state(sp, x >= 0.5, x0==1)

The second argument (x) refers to the outgoing state variable (i.e. the value at the end of the stage). The third argument (x0) refers to the incoming state variable (i.e. the value at the beginning of the stage). For users familiar with SDDP, SDDP.jl handles all the calculation of the dual variables needed to evaluate the cuts automatically behind the scenes.

The @state macro is just short-hand for writing:

@variable(sp, x >= 0.5)
@variable(sp, x0, start=1)
SDDP.statevariable!(sp, x0, x)

This illustrates how we can use indexing just as we would in a JuMP @variable macro:

X0 = [3.0, 2.0]
@state(sp, x[i=1:2], x0==X0[i])

In this case, both x and x0 are JuMP dicts that can be indexed with the keys 1 and 2. All the indices must be specified in the second argument, but they can be referred to in the third argument. The indexing of x0 will be identical to that of x.

There is also a plural version of the @state macro:

@states(sp, begin
    x >= 0.0, x0==1
    y >= 0.0, y0==1
end)

Standard JuMP machinery

Remember that sp is just a normal JuMP model, and so (almost) anything you can do in JuMP, you can do in SDDP.jl. The one exception is the objective, which we detail in the next section.

However, control variables are just normal JuMP variables and can be created using @variable or @variables. Dynamical constraints, and feasiblity sets can be specified using @constraint or @constraints.

The stage objective

If there is no stagewise independent uncertainty in the objective, then the stage objective (i.e. ignoring the future cost) can be set via the @stageobjective macro. This is similar to the JuMP @objective macro, but without the sense argument. For example:

@stageobjective(sp, obj)

If there is stagewise independent noise in the objective, we add an additional argument to @stageobjective that has the form kw=realizations.

kw is a symbol that can appear anywhere in obj, and realizations is a vector of realizations of the uncertainty. For example:

@stageobjective(sp, kw=realizations, obj)
setnoiseprobability!(sp, [0.2, 0.3, 0.5])

setnoiseprobability! can be used to specify the finite discrete distribution of the realizations (it must sum to 1.0). If you don't explicitly call setnoiseprobability!, the distribution is assumed to be uniform.

Other examples include:

# noise is a coefficient
@stageobjective(sp, c=[1.0, 2.0, 3.0], c * x)
# noise is used to index a variable
@stageobjective(sp, i=[1,2,3], 2 * x[i])

Dynamics with linear noise

SDDP.jl also supports uncertainty in the right-hand-side of constraints. Instead of using the JuMP @constraint macro, we need to use the @rhsnoise macro:

@rhsnoise(sp, w=[1,2,3], x <= w)
setnoiseprobability!(sp, [0.2, 0.3, 0.5])

Compared to @constraint, there are a couple of notable differences:

• indexing is not supported;

• the second argument is a kw=realizations key-value pair like the @stageobjective;

• the kw can on either side of the constraint as written, but when normalised to an Ax <= b form, it must only appear in the b vector.

Multiple @rhsnoise constraints can be added, however they must have an identical number of elements in the realizations vector.

For example, the following are invalid in SDDP:

# noise appears as a variable coefficient
@rhsnoise(sp, w=[1,2,3], w * x <= 1)

# JuMP style indexing
@rhsnoise(sp, w=[1,2,3], [i=1:10; mod(i, 2) == 0], x[i] <= w)

# noises have different number of realizations
@rhsnoise(sp, w=[1,2,3], x <= w)
@rhsnoise(sp, w=[2,3],   x >= w-1)

There is also a plural form of the @rhsnoise macro:

@rhsnoises(sp, w=[1,2,3], begin
    x <= w
    x >= w-1
end)
setnoiseprobability!(sp, [0.2, 0.3, 0.5])

Asset Management Example

We now have all the information necessary to define the Asset Management example in SDDP.jl:

using SDDP, JuMP, Clp

m = SDDPModel(
               # we are minimizing
                sense = :Min,
               # there are 4 stages
               stages = 4,
               # a large negative value
      objective_bound = -1000.0,
               # a MathOptBase compatible solver
               solver = ClpSolver(),
               # transition probabilities of the lattice
    markov_transition = Array{Float64, 2}[
                        [1.0]',
                        [0.5 0.5],
                        [0.5 0.5; 0.5 0.5],
                        [0.5 0.5; 0.5 0.5]
                    ],
               # risk measures for each stage
         risk_measure = [
                        Expectation(),
                        Expectation(),
                        EAVaR(lambda = 0.5, beta=0.5),
                        Expectation()
                    ]
                            ) do sp, t, i
    # Data used in the problem
    ωs = [1.25, 1.06]
    ωb = [1.14, 1.12]
    Φ  = [-1, 5]
    Ψ  = [0.02, 0.0]

    # state variables
    @states(sp, begin
        xs >= 0, xsbar==0
        xb >= 0, xbbar==0
    end)

    if t == 1 # we can switch based on the stage
        # a constraint without noise
        @constraint(sp, xs + xb == 55 + xsbar + xbbar)
        # an objective without noise
        @stageobjective(sp, 0)
    elseif t == 2 || t == 3
        # a constraint with noisein the RHS
        @rhsnoise(sp, φ=Φ, ωs[i] * xsbar + ωb[i] * xbbar + φ == xs + xb)
        # an objective with noise
        @stageobjective(sp, ψ = Ψ, -ψ * xs)
        # noise will be sampled as (Φ[1], Ψ[1]) w.p. 0.6, (Φ[2], Ψ[2]) w.p. 0.4
        setnoiseprobability!(sp, [0.6, 0.4])
    else # when t == 4
        # some control variables
        @variable(sp, u >= 0)
        @variable(sp, v >= 0)
        # dynamics constraint
        @constraint(sp, ωs[i] * xsbar + ωb[i] * xbbar + u - v == 80)
        # an objective without noise
        @stageobjective(sp, 4u - v)
    end
end

Solving the problem efficiently

During the solution process, SDDP.jl outputs some logging information (an example of this is given below). We briefly describe the columns:

The first column (Objective (Simulation)) is either a single value or a confidence interval from a Monte Carlo simulation (see MonteCarloSimulation). When the entry is a single value, its is the objective from a single (and the most recent) forward pass in SDDP. The single value is not an average. The second column (Objective (Bound)) is the deterministic bound of the problem (lower if minimizing, upper if maximizing). This is calculated every iteration. If a Monte Carlo simulation has been conducted this iteration, then the Objective (% Gap) will also be display. The objective gap is the relative percentage gap between the closest edge of the confidence interval and the deterministic bound.

The next two columns relate to the number of iterations (#) and time spend conducting them (Time). This information is printed every iteration. It does not include the time spent simulating the policy as part of the Monte Carlo simulation (i.e. to estimate the upper bound), or the time spent initializing the model.

The sixth and seventh columns relate to the Monte Carlo simulations. Specifically the number (#) of replications conducted, and time spent conducting them (Time). You can use these data to determine how often to perform the Monte Carlo simulations. For example, if the time is high relative to the iteration Cut Passes: Time, then you should perform the simulations less frequently.

Finally, Total (Time) is the total time (in seconds) of the solution process (including initialization).

Logging can be turned off by setting print level to 0. It can also be written to the file specified by the log file keyword.

-------------------------------------------------------------------------------
                      SDDP Solver. © Oscar Dowson, 2017.
-------------------------------------------------------------------------------
    Solver:
        Serial solver
    Model:
        Stages:         4
        States:         2
        Subproblems:    7
        Value Function: Default
-------------------------------------------------------------------------------
              Objective              |  Cut  Passes    Simulations   Total    
    Simulation        Bound   % Gap  |   #     Time     #    Time    Time     
-------------------------------------------------------------------------------
      -41.484         -9.722         |     1    0.0      0    0.0    0.0 
       -2.172         -7.848         |     2    0.0      0    0.0    0.0 
        4.284         -7.550         |     3    0.0      0    0.0    0.0 
      -10.271         -6.398         |     4    0.0      0    0.0    0.0 
  -7.782    -4.760    -6.346  -22.6  |     5    0.0    500    0.4    0.4 

                        ... some lines omitted ...

      -30.756         -5.570         |    29    0.1    1.9K   1.6    1.8 
  -7.716    -4.601    -5.570  -38.5  |    30    0.1    2.4K   2.0    2.2
  -------------------------------------------------------------------------------
    Statistics:
        Iterations:         30
        Termination Status: max_iterations
---------------------------------------------------------------------------------

Understanding the solution

... still to do ...

Simulating the policy

You can perform a Monte-Carlo simulation of the policy using the simulate function:

simulationresults = simulate(m, 100, [:xs, :xb])

simulationresults is a vector of dictionaries (one for each simulation). It has, as keys, a vector (with one element for each stage) of the optimal solution of xs and xb. For example, to query the value of xs in the third stage of the tenth simulation, we can call:

simulationresults[10][:xs][3]

Alternatively, you can peform one simulation with a given realization for the Markov and stagewise independent noises:

simulationresults = simulate(m, [:xs], markov=[1,2,1,1], noise=[1,2,2,3])

Visualizing the policy simulation

First, we create a new plotting object with SDDP.newplot(). Next, we can add any number of subplots to the visualization via the SDDP.addplot! function. Finally, we can launch a web browser to display the plot with SDDP.show.

See the SDDP.addplot! documentation for more detail.

Visualizing the Value Function

Another way to understand the solution is to project the value function into 3 dimensions. This can be done using the method SDDP.plotvaluefunction.

SDDP.plotvaluefunction(m, 1, 1, 0:1.0:100, 0:1.0:100;
    label1="Stocks", label2="Bonds")

This will open up a web browser and display a Plotly figure that looks similar to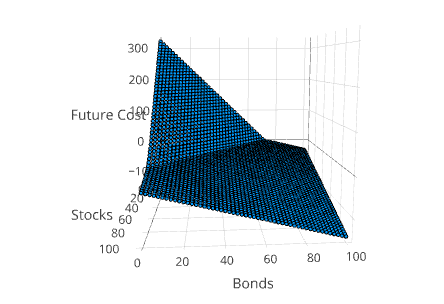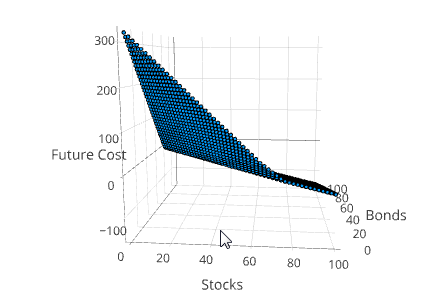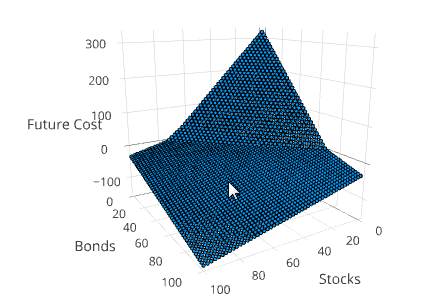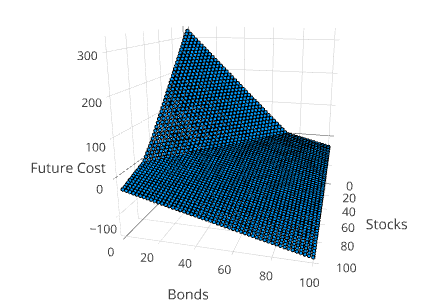

Saving models

Saving a model is as simple as calling:

SDDP.savemodel!("<filename>", m)

Later, you can run:

m = SDDP.loadmodel("<filename>")

Another (more persistent) method is to use the cut_output_file keyword option in SDDP.solve. This will create a csv file containing a list of all the cuts. These can be loaded at a later date using

SDDP.loadcuts!(m, "<filename>")

Extras for experts

New risk measures

SDDP.jl makes it easy to create new risk measures. First, create a new subtype of the abstract type SDDP.AbstractRiskMeasure:

struct MyNewRiskMeasure <: SDDP.AbstractRiskMeasure
end

Then, overload the method SDDP.modifyprobability! for your new type. SDDP.modifyprobability! has the following signature:

SDDP.modifyprobability!(
        measure::AbstractRiskMeasure,
        riskadjusted_distribution,
        original_distribution::Vector{Float64},
        observations::Vector{Float64},
        m::SDDPModel,
        sp::JuMP.Model
)

where original_distribution contains the risk netural probability of each outcome in observations occurring (so that the probability of observations[i] is original_distribution[i]). The method should modify (in-place) the elements of riskadjusted_distribution to represent the risk-adjusted probabilities of the distribution.

To illustrate this, we shall define the worst-case riskmeasure (which places all the probability on the worst outcome):

struct WorstCase <: SDDP.AbstractRiskMeasure end
function SDDP.modifyprobability!(measure::WorstCase,
        riskadjusted_distribution,
        original_distribution::Vector{Float64},
        observations::Vector{Float64},
        m::SDDPModel,
        sp::JuMP.Model
    )
    if JuMP.getobjectivesense(sp) == :Min
        # if minimizing, worst is the maximum outcome
        idx = indmax(observations)
    else
        # if maximizing, worst is the minimum outcome
        idx = indmin(observations)
    end
    # zero all probabilities
    riskadjusted_distribution .= 0.0
    # set worst to 1.0
    riskadjusted_distribution[idx] = 1.0
    # return
    return nothing
end

The risk measure WorstCase() can now be used in any SDDP model.

New cut oracles

SDDP.jl makes it easy to create new cut oracles. In the following example, we give the code to implmeent a cut-selection heuristic that only stores the N most recently discovered cuts. First, we define a new Julia type that is a sub-type of the abstract type SDDP.AbstractCutOracle defined by SDDP.jl:

struct LastCutOracle{N} <: SDDP.AbstractCutOracle
    cuts::Vector{SDDP.Cut}
end
LastCutOracle(N::Int) = LastCutOracle{N}(SDDP.Cut[])

LastCutOracle has the type parameter N to store the maximum number of most-recent cuts to return. The type has the field cuts to store a vector of discovered cuts. More elaborate cut-selection heuristics may need additional fields to store other information. Next, we overload the SDDP.storecut! method. This method should store the cut c in the oracle o so that it can be queried later. In our example, we append the cut to the list of discovered cuts inside the oracle:

function SDDP.storecut!(o::LastCutOracle{N},
        m::SDDPModel, sp::JuMP.Model, c::SDDP.Cut) where N
    push!(o.cuts, c)
end

Lastly, we overload the SDDP.validcuts method. In our example, the strategy is to return the N most recent cuts. Therefore:

function SDDP.validcuts(o::LastCutOracle{N}) where N
    return o.cuts[max(1,end-N+1):end]
end

The cut oracle LastCutOracle(N) can now be used in any SDDP model.